简单介绍如何使用PCA进行点云法向量估计
PCA用到的矩阵知识
- svd奇异值分解
- 瑞利熵
- 谱定理
PCA
- input:n*d,n代表个数,d代表维度
- Output:主成分向量 ,principle vectors ,仅仅是一个向量,代表一个方向。主成分的个数k<=原始空间维度数d
Q&A
- 什么是最主要的成分?
点的投影后分布的方差最大的方向。(在该方向上的点云分布的最分散) - 怎么获取第二个主成分
去掉第一个主成分之后分布方差最大的方向
法向量估计
1. 原理
所谓法线估计实质上就是对每一个点,在其邻域内估计出一个平面。
我们知道,估计一个平面需要一个点和一个法向量,这个法向量就是我们要估计的法向量。这个点就是这一群邻域点(与该点自身)的平均值。
设平均点为c,法向量为n,问题就可以转换到寻求一个方向n使得所有邻域点在方向n上的投影点的分布最为集中,这样一个优化问题,

很显然,根据PCA分析可以知道,寻求一个方向n使得所有邻域点在方向n上的投影点的分布最为集中,也是就意味着点在该方向上的投影的方差最小。这就是PCA中最不重要的那个方向向量,因为点云在三维空间所以,n就是第三个PCA向量。
我们选择c为这一群点的平均值,所以xi-c就是就是去中心化后的点。所以该问题变为了如下问题,
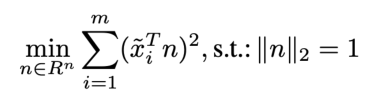
把括号展开,化简就可以得到
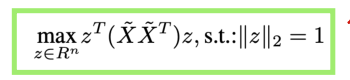
根据PCA可知,我们要求的n就是XXT最小特征值对应的特征向量。
2. 步骤
- 选择P
- 发现所选点的最近邻点
- PCA分析
- 法线:对应主成分中的最不重要的那一个方向(代表在该方向上的投影点分布最密集,方差最小)
- 曲率->最小特征值所占的比例
本文作者:
Su Yunzheng
本文链接: https://suyunzzz.github.io/2020/04/15/PCA主成分分析估计点云法向量(原理)/
版权声明: 本作品采用 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议 进行许可。转载请注明出处!

本文链接: https://suyunzzz.github.io/2020/04/15/PCA主成分分析估计点云法向量(原理)/
版权声明: 本作品采用 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议 进行许可。转载请注明出处!



